Les lois physiques
La loi de Mariotte (Principe général)
La loi de Mariotte (L'autonomie en air)
Tout le monde a déjà entendu parler de
pression (Hep garçon ! Une pression s'il vous plaît.. ) Bon, restons
sérieux. Voyons quelques exemples : La pression atmosphérique, la
pression des pneus, les boutons-pression, les nettoyeurs haute
pression....
Pour bien comprendre le principe physique de la pression, observons les
photos ci-dessous :
|
Si j'essaie d'enfoncer la lame d'un couteau du côté plat dans du beurre, c'est presque impossible. |
Par contre, si j'essaie avec le fil de la lame, le couteau rentre sans difficulté. |
Tentons d'expliquer le phénomène. Dans les
2 cas, nous avons appliqué la même force sur le couteau. Dans le premier
cas, la face d'appui de la lame étant grande, la pression était faible,
donc il n'y a pas eu pénétration de la lame. Dans le second cas, la
surface d'appui était faible (le fil de la lame) donc la pression était
plus grande et la pénétration de la lame facile.
Pour ceux qui sont proches des côtes de la Manche et par conséquent
proches des plages où il y a d'énormes grains de sable , ne tentez pas l'expérience
avec les galets, ça ne marche pas !
|
DÉFINITION |
|||
|
Une pression est le résultat d'une force appliquée sur une surface. Si P est la pression, F la force, S la surface
La pression augmente si :
|
Les unités :
-
La force s'exprime en kilogrammes (Kg),
-
La surface s'exprime en centimètres carrés (cm²),
-
la pression s'exprime en bars (b)
La pression atmosphérique (P. Atm) :
L'air à un poids. Oui, oui l'air pèse quelque chose, pas grand chose, mais quelque chose quand même. Soit : 1 litre d'air pèse environ 1,3 grammes. Sachant que la terre (la planète) est entourée d'air, nous subissons le poids de toute cette masse d'air. Cette pression est appelée pression atmosphérique. Cette pression varie en fonction de l'altitude. Plus on monte moins il y a de pression.
Au niveau de la mer, la pression atmosphérique est de 1 bar.
la pression hydrostatique (la pression dans l'eau) :
Nous avons vu que l'air avait un poids, l'eau aussi. 1Kg par litre. Lorsque nous allons nous immerger, nous allons subir cette pression. Cette pression sera d'autant plus importante que la quantité d'eau au dessus de vous sera épaisse. Le poids de cette eau est appelé pression relative.
|
|
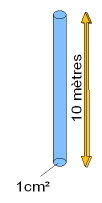
Une colonne d'eau de 10 mètres de haut et de 1 cm² de section exerce une pression de 1 bar. |
Donc, la pression relative à -10 mètres de profondeur est de 1 bar. A 20 mètres, 2 bars. A 30 mètres, 3 bars etc.
Mais dans l'eau ce n'est pas la seule pression que nous subissons, il ne faut pas oublier la pression atmosphérique qui au niveau de la mer est de 1 bar. Soit 1 bar de plus ! la somme de ces pressions est appelée pression absolue.

Pression absolue aux différentes profondeurs.
Conclusions :
Lors de la plongée, nous serons donc soumis à différentes pressions et si notre organisme résiste à cette pression c'est qu'il est constitué presque exclusivement de liquides (non déformables). Tout ça serait merveilleux si nous n'avions pas quelques cavités remplies d'air, il va donc falloir tout au long de nos plongées maintenir l'équilibre entre la pression ambiante et la pression de ses cavités (sinus).
Exercices
![]() :
:
Faites le calcul de la pression relative aux profondeurs suivantes : 15
mètres, 22 mètres, 3 mètres et 0,5 mètre.
![]() Pour avoir les résultats, cliquez et passez votre souris
entre les 2 guillemets " 2,5 bars ; 3,2 bars ;
1,3 bars ; 1,05 bars
"
Pour avoir les résultats, cliquez et passez votre souris
entre les 2 guillemets " 2,5 bars ; 3,2 bars ;
1,3 bars ; 1,05 bars
"
La loi de MARIOTTE (Principe général)
 Edme
MARIOTTE (1620-1684) physicien français (super la coupe de cheveux et en
faite, c'est un pote aux gars de la pub Chaussée aux Moiiiiiiiiiiines.... Amen).
Edme
MARIOTTE (1620-1684) physicien français (super la coupe de cheveux et en
faite, c'est un pote aux gars de la pub Chaussée aux Moiiiiiiiiiiines.... Amen).
La biographie d'Edme MAriotte est disponible sur le site Tout Dijon en suivant ce lien http://dijoon.free.fr/mariotte.htm .
Cette loi est appelée aussi loi de MARIOTTE - BOYLE. Robert BOYLE étant un physicien irlandais qui travailla à la même époque sur la compressibilité des gaz.
Nous l'avons aperçu tout à l'heure les liquides ainsi que les solides sont pratiquement incompressibles. Ce n'est pas le cas des gaz qui soumis à une pression diminuent de volume. Prenons quelques exemples : Un bloc de plongée peut contenir bien plus de litres d'air que son volume initial. C'est pareil pour un pneu de voiture. Un dernier exemple frappant, lorsque l'on gonfle la chambre à air d'un vélo et que l'on oublie de dévisser la valve, il est encore possible d'enfoncer le piston de la pompe. Et bien si à la place vous mettez de l'eau ce sera impossible.
Expérience :
Faisons une petite expérience. Prenons un verre gradué (vous savez, pour faire les crêpes !), retournons-le et enfonçons-le progressivement dans l'eau. L'eau va monter lentement à l'intérieur du verre, comprimant l'air qu'il contient. À 10 mètres de profondeur (la pression absolue est à 2 bars), l'air n'occupe plus que la moitié du volume. Si nous continuons à enfoncer le verre jusqu'à 30 mètres (la pression absolue est à 4 bars), l'eau occupe maintenant les 3/4 du verre. Que se passe-t-il si nous remontons le verre? La pression va diminuer, l'air va se dilater et chasser l'eau. De retour à la surface, l'air occupe tout le volume.
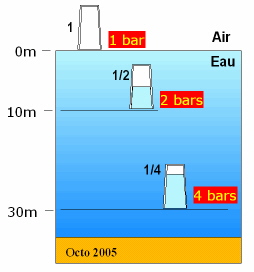
Démonstration
On voit ainsi que le volume d'un gaz est inversement proportionnel à la pression qu'il reçoit. C'est la loi de MARIOTTE.
|
DÉFINITION |
|||||
|
La loi de MARIOTTE peut s'exprimer de 2 façons avec : P1 est la pression avant immersion, V1 est le volume du gaz avant immersion, P2 est la pression en immersion, V2 est le volume du gaz en immersion
Ou,
P1 x V1 = P2 x V2 = constante
Cette loi précise que ceci est
vrai à température constante., mais en plongée, la variation
de température est trop faible pour en tenir compte. |
Les unités :
-
Le volume s'exprime en litres (l),
-
la pression s'exprime en bars (b).
Mise en application :
Vérifions cette loi avec un ballon de baudruche (les ballons dans les mariages). Gonflons ce ballon avec 6 litres d'air.
P = 1 bar V = 6 litres donc P x V = 6
Immergeons ce ballon à 10 mètres, le ballon a diminué de moitié :
P1 = 2 bars V1 = 3 litres donc P1 x V1 = 6
Immergeons ce ballon à 30 mètres, le ballon n'a plus que le quart de son volume initial :
P2 = 4 bars V2 = 1,5 litres donc P2 x V 2= 6
A 70 mètres le ballon n'a plus que le 8éme de son volume initial :
P3 = 8 bars V3 = 0,75 litre donc P3 x V3 = 6
Conclusions :
Cette mise en application nous permet de mettre en évidence que, dans les 10 premiers mètres, les variations relatives de volume et de pression sont proportionnellement plus importantes qu'en profondeur.
En effet, entre 0 et -10 mètres, la pression double et le volume diminue de moitié. Mais il faut attendre ensuite 20 mètres de plus, puis 40 de plus pour obtenir la même proportion.
Exercices
![]() :
:
1) Un parachute pour remonter une ancre est gonflé avec 10 litres d'air à -20 mètres de profondeur. Quel volume d'air aura-t-il en atteignant la surface ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
A - 20 mètres il y a 3 bars donc (P1 x V1 = cst) 3
x 10 = 30. A la surface il y a 1 bar alors (P2 x V2 = Cst) 1 x ?? = 30
d'où 30 / 1 = 30. Le volume d'air à la surface sera de 30 litres
"
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
A - 20 mètres il y a 3 bars donc (P1 x V1 = cst) 3
x 10 = 30. A la surface il y a 1 bar alors (P2 x V2 = Cst) 1 x ?? = 30
d'où 30 / 1 = 30. Le volume d'air à la surface sera de 30 litres
"
2) Un parachute a une capacité de 30 litres. À 38 mètres j'insuffle avec mon octopus 12 litres d'air. Arrivé à la surface l'air débordera-t-il du parachute ? si oui, à quelle profondeur commencera-t-il à déborder ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
À -38 m la pression est de 4,8 bars donc (P1 x V1 = cts) 4,8 x 12 =
57,6. A la surface il y a 1 bar donc (P2 x V2 = cst) 1 x ??? = 57,6 d'où
57,6 / 1 = 57,6 litres théoriques à la surface. 57,6 > 30 donc le
parachute déborde. Pour trouver à quel profondeur il va déborder, très
simple (P3 x V3 = cst) ??? x 30 = 57,6 d'où 57,6 / 30 = 1,92 bars il
débordera à - 0, 92 mètre."
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
À -38 m la pression est de 4,8 bars donc (P1 x V1 = cts) 4,8 x 12 =
57,6. A la surface il y a 1 bar donc (P2 x V2 = cst) 1 x ??? = 57,6 d'où
57,6 / 1 = 57,6 litres théoriques à la surface. 57,6 > 30 donc le
parachute déborde. Pour trouver à quel profondeur il va déborder, très
simple (P3 x V3 = cst) ??? x 30 = 57,6 d'où 57,6 / 30 = 1,92 bars il
débordera à - 0, 92 mètre."
3) Un bloc de 12 litres est gonflé à 230 bars. Combien de m³ d'air cela représente, une fois détendus à la surface ? (Il faut 1 000 litres pour faire 1 m³).
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "À
230 bars le volume est de 12 litres (P1 x V1 = Cst) 230 x 12 = 2 760,
donc à la surface, à 1 bar on a la relation suivante (P2 x V2 = Cst) 1 x
??? = 2 760 soit 2 760 / 1 = 2760 litres. le volume d'air détendu est
donc 2 760 / 1 000 = 2,76
m³
"
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "À
230 bars le volume est de 12 litres (P1 x V1 = Cst) 230 x 12 = 2 760,
donc à la surface, à 1 bar on a la relation suivante (P2 x V2 = Cst) 1 x
??? = 2 760 soit 2 760 / 1 = 2760 litres. le volume d'air détendu est
donc 2 760 / 1 000 = 2,76
m³
"
La loi de Mariotte (L'autonomie en air)
Le second volet de la loi de Mariotte traite de l'autonomie en air en plongée sous-marine. Pour commencer, je vais vous parler d'apnée. Rien à voir avec le sujet vous allez me dire, et bien si. Vous savez tous respirer avec un tuba ? Oui, bien sûr puisque vous êtes minimum niveau 1. Avez-vous fait l'expérience de vous mettre verticalement dans la piscine en PMT (palmes, masque, tubas), la tête sous l'eau, avec juste le bout du tuba qui dépasse de la surface ? Oui ? Non ? Et bien vous avez dû vous rendre compte qu'il était difficile de respirer, alors que lorsque l'on nage à plat, il n'y a aucun problème.
Explication du phénomène :
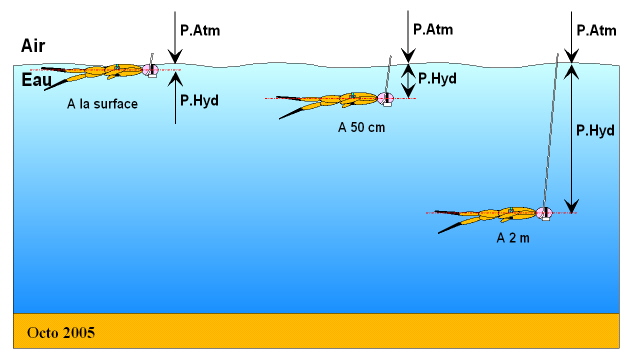
Avec un tuba classique de 30 cm de long, on
peut aisément respirer à la surface, la tête sous l'eau. A ce niveau
d'immersion, la pression totale supportée par le thorax du plongeur est
(la pression atmosphérique + pression hydrostatique) soit 1 bar + 0,03
bar = 1,03 bars.
À -50 cm sous l'eau, la respiration devient très difficile 1 bar + 0,05
bar = 1,05 bars.
A 2 mètres, la respiration est impossible. Ceci est dû au fait que l'air
apporté par le tuba est à la pression atmosphérique alors que la cage
thoracique est soumise à la pression hydrostatique qui est beaucoup plus
importante. 1 bar + 0,2 bar = 1,2 bars. Le plongeur est capable
d'expirer, mais incapable d'inspirer du fait de la pression
atmosphérique trop faible.
En conclusion, pour que le plongeur puisse respirer, il faut que l'air qui lui parvient arrive à la pression ambiante (où il se trouve). C'est pourquoi les détendeurs délivrent toujours de l'air à la pression ambiante.
Un plongeur consomme un volume environ 0,5 à 3 litres à chaque inspiration à la pression atmosphérique (à la surface ) et consomme approximativement la même quantité d'air en plongée. Donc, la quantité d'air inspirée sera d'autant plus importante que la profondeur (pression ambiante) sera grande.
Exemples :
La consommation moyenne d'air d'un plongeur est de 20 litres d'air par minutes.
-
20 l / min. à 1 bar = 20 l / min. en surface,
-
20 l / min. à 2 bars = 40 l / min. à 10 mètres,
-
20 l / min. à 3 bars = 60 l / min. à 20 mètres,
-
20 l / min. à 5 bars = 100 l / min. à 40 mètres.
Exercices
![]() :
:
1) Nous plongeons sur l'épave du Berkeley gisant par 20 m de fond. Combien de temps pouvons-nous plonger avec un bloc de 12 litres gonflé à 220 bars, si l'on décide d'interrompre la plongée, pour la remontée, à 50 bars ? (On ne tient pas compte de la consommation pour la descente et la consommation de référence est de 20 l / minute.)
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"
En premier, je calcule l'air disponible :
(220 b -50b de réserve) x 12 litres = 2 040 litres.
En second,
la consommation : 20 l/min. x 3 bars (PA à 20 mètres) = 60 l/ min. donc
2 040 l / 60 l/ min. = 34 min.
On peut donc rester 34 minutes à 20 mètres sur le Berkeley."
2) Le lendemain, chouette ! On replonge sur le Berkeley, accompagné d'un moniteur qui nous apprendra le maniement d'un parachute pour remonter l'ancre. Cette fois-ci, c'est marée haute et la profondeur est de 27 mètres. Le mono qui est super sympa m'a prêté son bloc de 15 litres à 230 bars. Il m'a indiqué qu'il faudrait mettre 10 litres d'air dans le parachute pour faire décoller l'ancre du fond et qu'i faudra interrompre la plongée à 50 bars. Combien de temps va-t-on pouvoir plonger ? (On ne tient pas compte de la consommation pour la descente et la consommation de référence est de 20 l / minute.)
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"
En premier, je calcule l'air disponible :
(230 b - 50 b de réserve) x 15 litres = 2 700 litres. Je dois mettre 36
litres côté pour le parachute donc 2 700 - 36 = 2 664 litres
En second,
la consommation : 20 l/min. x 3,7 bars (PA à 27 mètres) = 74 l/ min.
donc 2 664 l / 74 l/ min. = 36 min.
On peut donc rester 34 minutes à 20 mètres sur le Berkeley."
 Archimède
(287-212 av. J.-C.), mathématicien, physicien et ingénieur grec. Tout le
monde a entendu parler un jour du théorème d'Archimède, avec plus ou
moins de bonheur d'ailleurs. Car les récupérations de ce théorème sont
nombreuses je préfère vous les énoncer tout de suite, comme ça, cela
sera fait ! Alors, commençons : 1er) Tout corps plongé dans un liquide
ressort mouillé, 2ème) Tout corps plongé dans dans l'eau ressort au bout
d'un certain temps, 3ème) Tout corps plongé dans un liquide finit
toujours par avouer et 4ème et la dernière) Tout corps plongé dans un
liquide est toujours dérangé par le téléphone. (P. Desproges.)
Archimède
(287-212 av. J.-C.), mathématicien, physicien et ingénieur grec. Tout le
monde a entendu parler un jour du théorème d'Archimède, avec plus ou
moins de bonheur d'ailleurs. Car les récupérations de ce théorème sont
nombreuses je préfère vous les énoncer tout de suite, comme ça, cela
sera fait ! Alors, commençons : 1er) Tout corps plongé dans un liquide
ressort mouillé, 2ème) Tout corps plongé dans dans l'eau ressort au bout
d'un certain temps, 3ème) Tout corps plongé dans un liquide finit
toujours par avouer et 4ème et la dernière) Tout corps plongé dans un
liquide est toujours dérangé par le téléphone. (P. Desproges.)
Voilà, c'est fait, maintenant on va pouvoir passer aux choses
sérieuses... Pour ceux que la biographie d'Archimède intéresse, je vous
conseille le site Pi (ça ne s'invente pas !) disponible sur ce lien http://www.peripheria.net/bios/archimede/ . Très intéressant avec
plein de photos d'époques ???
Expérience :
Passons à la petite expérience. Imaginez un cube indéformable de poids nul et de 10 cm de côté, soit 1 décimètre cube (1 dm³ = 1 litre).
Insérons dans ce cube un poids de 500 grammes et plongeons-le dans l'eau, il flotte. Rajoutons aux premiers 500 g, 500 g de plus. Le cube se maintient entre deux eaux, il est en équilibre quelle que soit la profondeur. Ajoutons maintenant, 500 g de plus (500 +500 +500), il coule ! En effet, 1 décimètre cube c'est le volume qu'occupe 1 litre d'eau. Et un litre d'eau pèse 1 Kg.
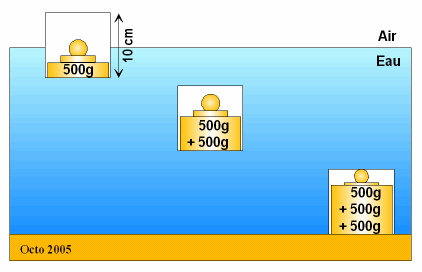
Démonstration
Nous constatons que :
Si le cube est plus léger que la quantité d'eau ayant le même volume que lui, il flotte;
S'il pèse le même poids, il est en équilibre;
S'il est plus lourd, il coule.
Ce principe est vrais quel que soit le corps immergé. Il a été énoncé par Archimède de la façon suivante (la vraie).
«Tout corps plongé dans un liquide reçoit de la part de celui-ci une poussée verticale, dirigée du bas vers le haut, égal au poids du volume déplacé.»
Cette poussée est appelée poussée d'Archimède.
|
DÉFINITION |
|
|
Appelons poids réel (PR) le poids d'un corps dans l'air et poids apparent (PA) le poids d'un corps dans l'eau. Ce poids apparent est la différence entre le poids réel et la poussée d'Archimède (P. Archi.)
PA = PR - P.Archi
Poids apparent = poids réel - Poussée d'Archimède
Si le poids apparent est :
|
Application du théorème d'Archimède à la plongée par l'exemple :
-
Un plongeur qui revêt sa combinaison de plongée isothermique faite de néoprène (caoutchouc alvéolaire plus léger que l'eau), augmente son volume et la poussée d'Archimède est nettement plus forte que s'il était en maillot de bain. Pour compenser cette poussée, il doit placer sur sa ceinture des plombs qui ont un volume beaucoup plus faible pour un poids plus important. Le nombre de plombs doit compenser exactement la poussée d'Archimède. Souvenez-vous on à vu quelque chose comme ça dans les cours niveau 1 (voir l'exemple dans une nouvelle fenêtre ici ).
-
Un plongeur bien équilibré dans l'eau, s'il respire à fond, il remonte. S'il expire à fond, il descend (souvenez-vous le poumon ballaste ça vous rappel quelque chose?).
-
De la même manière, vous savez faire la planche ? On se met sur le dos les poumons bien remplis et on tient à la surface. Si on expire à fond, on coule.
-
Dans les opérations de remontée d'objet du fond (une ancre, un bloc de pierre, votre belle mère? Non on la laisse au fond !) on utilise une enveloppe souple appelée parachute, dans laquelle on introduit de l'air, déplaçant un volume d'eau équivalant et recevant donc une poussée ascendante qui va servir à vaincre l'effet du poids apparent de l'objet à remonter. Pour votre information, il n'existe pas, dans le commerce, des parachutes pour belle-mère).
Il n'y a pas de lien si vous cliquez
sur la belle mère, donc ne cliquez pas dessus.
Merci pour elles !
Calculons un exemple concret :
Un corps-mort (c'est le nom que l'on donne aux moyens pour amarrer les bateaux) est constitué d'un bloc de béton de 1 m x 1 m x 0,5 m. La densité du béton utilisé est de 4 (1 pour l'eau). Quel volume d'air devra-t-on introduire dans un parachute de relevage pour équilibrer l'ensemble ? (Généralement dans les problèmes on néglige les poids et les volumes du parachute et des bouts (on dit "bout" dans la marine et pas corde).
En premier, on calcul le poids réel du bloc de béton :
1 ) le volume : 1 x 1 x 0,5 = 0, 5 m³
2) poids réel : 0,5 m³ x 4 T/m³ = 2 T (2 000 Kg)
Poussée d'Archimède subie : poids de 0,5 m³ d'eau soit 500 kg
Sont poids apparent est de :
Poids réel - poussée d'Archimède = 2 000 - 500 = 1 500 Kg
L'air introduit dans le parachute doit équilibrer le poids apparent du corps mort. Il nous faut donc 1 500 litres d'air qui déplaceront les 1 500 litres d'eau en créant une poussée ascendante de 1 500 Kg.
Exercices
![]() :
:
1) Un objet a un volume de 4,2 dm³ et pèse 6 500 grammes. Quel sera son poids apparent dans l'eau et que fera-t-il ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
PA = PR -
P.Archi -> ??? = 6 500 g - 4 200 m³ =
2 300 grammes. Il coule."
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
PA = PR -
P.Archi -> ??? = 6 500 g - 4 200 m³ =
2 300 grammes. Il coule."
2) Préambule : ne pas suivre cet exemple, on ne doit pas remonter d'amphore. Un plongeur découvre par 40 mètres de fond une amphore, pleine et bouchée, dont le poids réel est de 25 Kg et de volume extérieur 15 dm³. Pour la remontée, il y attache, un parachute d'une densité gale à 1, et y introduit 8 litres d'air. Il la décolle du fond en palmant. À partir de quelle profondeur pourra-t-il la lâcher, le parachute pouvant seul, la faire remonter ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"PA =
PR - P.Archi -> ??? = 25 -15 , PA = 10. Utilisation de la loi de
Mariotte. A 40 mètres la pression est de 5 bars. P1 x V1 = P2 x V2
-> 5 x 8 = ??? x 10 = 40 / 10 = 4 bars. La profondeur à 4 bars est
de 30 mètres."
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"PA =
PR - P.Archi -> ??? = 25 -15 , PA = 10. Utilisation de la loi de
Mariotte. A 40 mètres la pression est de 5 bars. P1 x V1 = P2 x V2
-> 5 x 8 = ??? x 10 = 40 / 10 = 4 bars. La profondeur à 4 bars est
de 30 mètres."
 Déjà
qu'il y en a qui ne voient rien en surface, alors dans l'eau...
Déjà
qu'il y en a qui ne voient rien en surface, alors dans l'eau...
Notre oeil est conçu pour fonctionner dans l'air, dans l'eau il n'arrive
pas à faire la mise au point et l'on voit trouble.
Pour retrouver une image nette, il suffit d'interposer, entre l'oeil et l'eau, une couche d'air. C'est le rôle du masque.
Déformation de la vision :
Lorsque le plongeur utilise un masque, la lumière traverse 2 milieux différents : L'eau puis l'air. Au passage de l'un à l'autre les rayons sont déviés, on parle de réfraction. Cela se traduit par 2 incidences :
1) L'angle sous lequel nous voyons les objets dans l'eau est plus grand qu'à l'air libre. Il y a grossissement d'un facteur de 4/3.
2) Il y a diminution des distances.
Les choses apparaissent plus proches d'un facteur de 3/4.
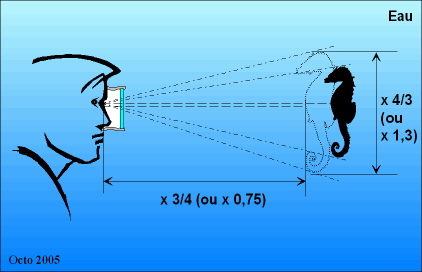
La Vision sous l'eau
Un truc :
Un moyen mnémotechnique pour se rappeler si l'on emploie le bon facteur (3/4 ou 4/3). Tout le monde sait que tous
les plongeurs prétendent avoir vu un poisson "GRAND COMME ÇA ", donc
plus gros que réellement, alors vous prenez la taille du poisson,
1 mètre par exemple, vous le diviser par 4/3, si la taille du poisson
réduit, c'est le bon facteur ! (1 m x 4/3 = 1,30 mètres). si on
divise par l'autre facteur (3/4), il s'agrandit c'est le mauvais
facteur.
Rétrécissement
du champ de vision
:
Le champ de vision avec un masque est réduit de 50% à 70% suivant les modèles. Ce rétrécissement se produit sur les côtés, mais aussi au-dessus et en dessous.
Les incidences sont multiples : Pour regarder
autour de soi, tourner la tête ne suffit pas, il faut faire tourner
tout son corps. Trouver les purges de son gilet, son parachute de palier,
son octopus, son mano... se font généralement sans voir directement
l'élément. D'où la nécessité d'acquérir des automatismes. Les signes de
communication doivent être faits à la hauteur du masque pour que votre
interlocuteur puisse les voir.
La lumière :
Vous avez dû remarquer que sous l'eau, généralement, nous avons besoin d'un phare ou d'une lampe et sans forcément faire une plongée de nuit. Quoique je me souviens avoir fait au large de Dieppe des plongées de nuit le jour, mais ça, c'est une autre histoire ! Donc, je disais donc, on a souvent besoin d'un phare et la raison est très simple : les rayons lumineux qui franchissent la surface ne parviennent pas jusqu'à vous. Soit ils sont réfléchis à la surface de l'eau, soit il sont réfléchis sur des particules en suspension. Hélas, c'est autant de luminosité de perdue pour nous plongeurs.
Des calculs ont été réalisés sur la base d'une luminosité de 100 % en surface : il n'en reste que 40 % à 1 mètre, 14 % à 10 mètres 7 % à 20 mètres et seulement 1,5 % à 40 mètres.
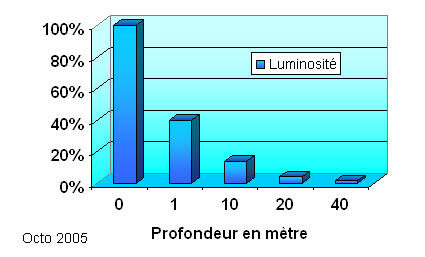
Les couleurs :
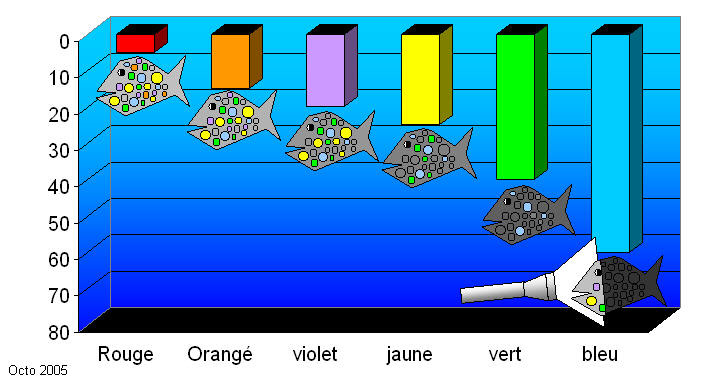
Lors de vos plongées vous avez pu constater que les couleurs étaient différentes sous l'eau, cette différence vient de l'absorption des des rayons lumineux. Ce qui fait que plus l'on descend, plus les couleurs son absorbées. Chacune des couleurs disparaît à une profondeur particulière.
-
Les rouges disparaissent vers 5 mètres.
-
Les orangés vers 10 à 15 mètres.
-
Les violets vers 20 mètres.
-
Les jaunes vers 15 à 25 mètres.
-
Les verts au-delà des 40 mètres pour ne laisser que du bleu.
Info :
Pour les bigleux et les bigleuses, il est possible de se faire faire un masque à sa vue. Les prix sont maintenant abordables et les verres peuvent être même remboursés par certaines mutuelles. Un conseil, si vous souhaitez investir dans un masque à votre vue, préférez un masque de marque pour être sur de retrouver des pièces détachées s'il arrivait un accident (jupe qui se déchire par exemple).
Exercices
![]() :
:
1) Un jeune plongeur vous dit qu'il a vu un congre de 3 mètres. Que lui direz-vous sur sa dimension réelle ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
3 mètres / par
4/3. En réalité le poisson ne devait ne faire que 2,30 mètres à-tout-casser !"
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
3 mètres / par
4/3. En réalité le poisson ne devait ne faire que 2,30 mètres à-tout-casser !"
2) Vous faites des exercices de signes avec votre meilleure amie plongeuse et elle vous demande une assistance. A vu de nez, elle se trouve à 2 mètres. Quelle est sa distance réelle ?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"2 mètres x par 3/4. La
jolie plongeuse se trouve en réalité beaucoup plus proche de vous....
puisqu'elle n'est en fait qu' à un tout-petit mètre cinquante du bel
apollon. Mais ce n'est pas le moment d'en profiter, on est là pour les
exercices !"
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets
"2 mètres x par 3/4. La
jolie plongeuse se trouve en réalité beaucoup plus proche de vous....
puisqu'elle n'est en fait qu' à un tout-petit mètre cinquante du bel
apollon. Mais ce n'est pas le moment d'en profiter, on est là pour les
exercices !"
 L'acoustique
en milieu aérien est dû aux vibrations mécaniques de l'air. Ses
sollicitations mécaniques font vibrer nos tympans. Par temps calme la
vitesse de ses vibrations dans l'air est de l'ordre de 330 m / seconde.
Dans l'eau, la vitesse est grandement supérieure et approximativement de
1 400 m / seconde.
L'acoustique
en milieu aérien est dû aux vibrations mécaniques de l'air. Ses
sollicitations mécaniques font vibrer nos tympans. Par temps calme la
vitesse de ses vibrations dans l'air est de l'ordre de 330 m / seconde.
Dans l'eau, la vitesse est grandement supérieure et approximativement de
1 400 m / seconde.
Cette différence de vitesse vient de la densité du milieu ou se propage les ondes (Air/eau).
En plongée, ce changement de vitesse aura pour conséquence de ne plus pouvoir identifier l'origine des sons. En effet, dans l'air, notre cerveau calcul la différence du temps de perception entre l'oreille droite et gauche avec un facteur de 330 m / seconde, ce qui nous permet de localiser l'origine (droite /gauche / avant / arrière) . Dans l'eau notre cerveau ne peut plus calculer cette différence, on entend le son, mais on ne sait pas d'où il provient.
Exercices
![]() :
:
1) Une explosion sous-marine se produit à 14 Km du lieu de plongée. Au bout de combien de temps les plongeurs immergés et le pilote sur le bateau.?
![]() Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
L'explosion a
lieu à 14 000 mètres. Sous l'eau le bruit de l'explosion arrivera 14 000
m / 1 400 m / s = 10 secondes. Pour le pilote, 14 000 m /
330 m / s = 42 secondes."
Pour avoir
les résultats, cliquez et passez votre souris entre les guillemets "
L'explosion a
lieu à 14 000 mètres. Sous l'eau le bruit de l'explosion arrivera 14 000
m / 1 400 m / s = 10 secondes. Pour le pilote, 14 000 m /
330 m / s = 42 secondes."